Published
Late-time behaviors of scalar field modes for a collapsing null shell spacetime and for the Unruh state in Schwarzschild spacetime (with P Anderson and A Fabbri),
Infrared effect and the Unruh state (with P Anderson and Z Scofield),
Method to compute the stress-energy tensor for a quantized scalar field when a black hole forms from the collapse of a null shell (with P Anderson, R Clark, and A Fabbri),
Stress-energy tensor for a quantized scalar field in a four-dimensional black hole that forms from the collapse of a null shell (with P Anderson, R Clark, and A Fabbri),
Proceedings of the sixteenth Marcel Grossmann Meeting on General Relativity
Preprint
On the convergence of the variational iteration method applied to variable coefficient Klein-Gordon problems (with S Robinson)
On the convergence of the variational iteration method applied to variable coefficient Klein-Gordon problems II (with P Drabek and S Robinson)
Under Preparation
Mean exit time for perturbed gradient systems (with J Gemmer)
Semi-classical stress-energy tensor in a spherically symmetric null shell (with P Anderson and A Fabbri)
Quantum effects in the interiors of two-dimensional black hole spacetimes (with P Anderson and A Peake)
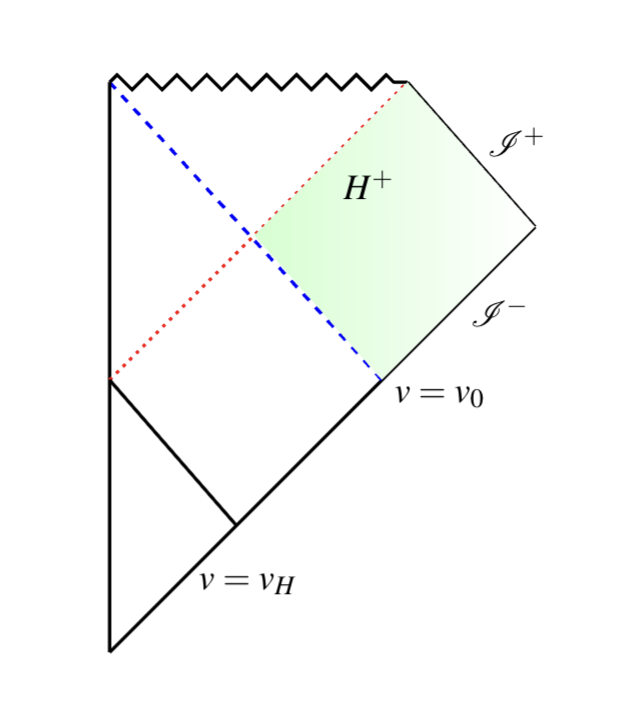
Consider a shell a photons originating from infinity that gravitationally collapses and forms a 4D black hole. The picture above shows the Penrose diagram of such spacetime. We developed a method that can be used to find the stress-energy tensor for a quantum field outside the horizon of such black hole. Mathematically speaking, our method involves finding the solution to a Klein-Gordon equation in the black hole spacetime and renormalizing the stress-energy tensor.
In his original calculation, Hawking showed that in a time-dependent geometry (he considered a black hole that formed from gravitational collapse), particle production occurs once the quantum effects are taken into account. It is mathematically much simpler to study quantum effects in static and stationary spacetimes. There are typically three states for the quantum fields that are considered for eternal black holes, one of which is the Unruh state which mimics the Hawking effect in eternal black holes. We studied the detailed behaviors of the modes of quantized scalar fields in the Unruh state for various 2D eternal black holes . We showed that the late time behaviors of the modes of the quantum fields and of the symmetric two-point function are determined by infrared effects.
In this research work, we have studied the late-time behaviors of modes which make up a quantum field in the Unruh state in Schwarzschild spacetime and the modes of a quantized field in the vacuum state in a 4D black hole (we call these in modes) that forms from the gravitational collapse. We showed that the in modes approach the Unruh modes at late times as a power law in time preceded by a period of oscillations that appear to be due to quasi-normal modes.
to be appeared in Physical Review D